PCA(Partial Component Analysis, 主成分分析)は多次元データの可視化手法の中で多用される手法の一つです。世の中には様々な可視化手法がありますが、最も手軽で分かりやすいのがこの手法ではないでしょうか。この記事では、PCAについて簡単に説明し、Scikit-Learnを利用した基本的な使い方を整理します。
PCAの理論を把握するにあたり、筆者が主に使用したのは「はじめてのパターン認識」です。但し、この記事では詳しい内容は扱わないので、気になる方は教科書を読んで見てください。
概要
まずはPCAとは何かを簡単に確認しておきます。
参考文献をお借りすると、主成分分析は「分散が最大になる方向への線形変換を求める手法」(平井有三著、「はじめてのパターン認識」 P. 137より引用)と説明されます。
また、Scikit-Learnのライブラリでは、”Linear dimensionality reduction using Singular Value Decomposition of the data to project it to a lower dimensional space.”(sklearn.decomposition.PCAのドキュメントより引用)、意訳すると、「データの特異値分解を利用した、より低い空間への射影のための線形な次元削減手法」と紹介されています。
変換そのものか次元削減かどちらに主眼を置いているかで説明のニュアンスがなんとなく異なっているような印象を受けるかもしれませんが、どちらも間違いではなく、「主成分分析を利用した次元削減」と考えておくと良いのではないかと思います。
要は、なるべくデータの広がり方が明確に見えるような軸を見つけ出して変換することができる手法で、PCAを利用することで、分散に基づくデータの違いが見やすい形で低次元に落とし込むことができる、と考えておくと良いのではないかと思います。
詳しい説明については、参考文献等をご参照ください。
PCA使用前の前処理について
PCAは分散を最大化するような変換を求めるので、事前に標準化しておくことが多いです。これにより、単位が異なる様々な系列に対してより公平に分散を評価することができます。
場合によっては標準化を使用しないこともあるようです。例えば、初めから単位が同じ系列で、その中での分散を評価して次元削減に持ち込みたい、という場合がこの例に当たるようです。詳しくはこちらで議論されていたので、ご参照ください。https://www.quora.com/Is-standardization-and-normalization-the-same-in-PCA-When-should-or-should-not-we-normalize-data-in-PCA
実際上は標準化する場合が多いと思いますが、自分の目的に合わせて理由を踏まえた上で実施していれば特に問題ないかと思います。
コード例
今回の目的はPCAの使い方を確認することなので、簡単に実施したいと思います。
使うデータはWine Quality Data Setの赤ワインのデータです。ただし、全てのデータを使うとあまり上手く情報を分けることができなかったので、今回は対象とするデータを”quality”を使って絞りながらトライアルを行いました。
また、描画手法などについては、Scikit-Learnにあるサンプルである下記の資料を参考にしました。
https://scikit-learn.org/stable/auto_examples/datasets/plot_iris_dataset.html#sphx-glr-auto-examples-datasets-plot-iris-dataset-py
quality(4, 7)に対するPCA
Wine-qualityデータセットには3から8まで6種類のqualityがあります。
3と8は数としてかなり少ないので、残りの4、5、6、7の4種類から、まずは違いが分かりやすいと思われる4と7を比較します。今回は平面に描画するため、引数のn_componentsは2に設定します。
コードと結果は下記の通りです。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
data_path = "../input/wine-quality/winequality-red.csv"
wine_red_df = pd.read_csv(data_path, sep=";")
# 目的変数がqualityなので、qualityを外したデータを描画
use_cols = wine_red_df.columns.tolist()[:-1]
scaler = StandardScaler()
reduced_df = wine_red_df[wine_red_df["quality"].isin([4, 7])]
train_df = reduced_df[use_cols]
scaled_df = scaler.fit_transform(train_df)
labels = reduced_df["quality"]
pca = PCA(n_components=2)
pca.fit(scaled_df)
pca_results = pca.transform(scaled_df)
結果は下記の通りです。
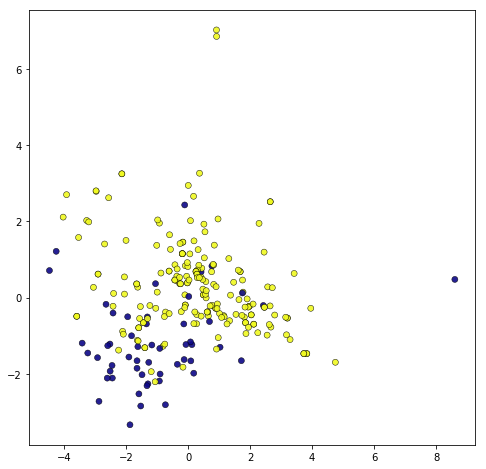
ライブラリのimportから記載したので長くなってしまいましたが、実施していることは非常に簡単な内容でした。
quality(5, 6)に対するPCA
今度は、qualityが5のデータと6のデータに対してPCAを実施します。
scaler = StandardScaler()
reduced_df = wine_red_df[wine_red_df["quality"].isin([5, 6])]
train_df = reduced_df[use_cols]
scaled_df = scaler.fit_transform(train_df)
labels = reduced_df["quality"]
pca = PCA(n_components=2)
pca.fit(scaled_df)
pca_results = pca.transform(scaled_df)
fig, ax = plt.subplots(figsize=(8,8))
ax.scatter(pca_results[:, 0], pca_results[:, 1], c=labels, alpha=0.8,
linewidth=0.5,edgecolors="k", cmap=plt.cm.plasma)
結果のグラフはこちらです。
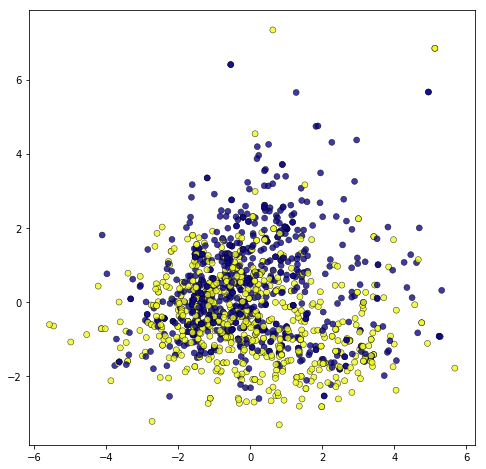
これは中々分かりづらい結果になってしまいました。
2次元でダメだったので3次元も試してみたいと思います。主要な変更は、引数のn_componentsを3にするところと、3次元のグラフ描画のためのライブラリや設定を行なっているところです。後者については詳しくはここでは扱いません。
from mpl_toolkits.mplot3d import Axes3D
scaler = StandardScaler()
reduced_df = wine_red_df[wine_red_df["quality"].isin([5, 6])]
train_df = reduced_df[use_cols]
scaled_df = scaler.fit_transform(train_df)
labels = reduced_df["quality"]
pca = PCA(n_components=3)
pca.fit(scaled_df)
pca_results = pca.transform(scaled_df)
fig = plt.figure(1, figsize=(8,6))
ax = Axes3D(fig, rect=[0, 0, 0.8, 0.8], elev=30, azim=60)
ax.scatter(pca_results[:, 0], pca_results[:, 1], pca_results[:, 2], c=labels, alpha=0.5,
linewidth=0.5,edgecolors="k", cmap=plt.cm.plasma)
ax.w_xaxis.set_label_text("First")
ax.w_yaxis.set_label_text("Second")
ax.w_zaxis.set_label_text("Third")
plt.show()
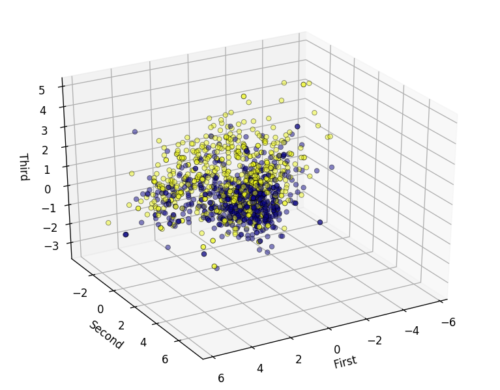
3次元で描画したグラフはこちらです。
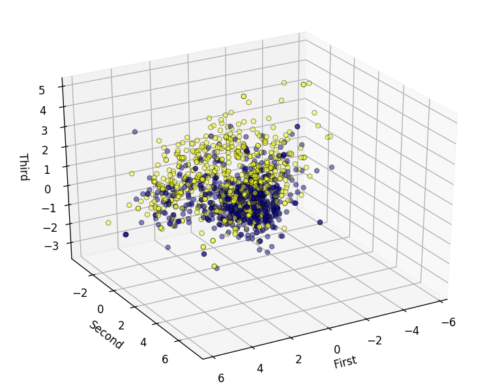
2次元で見るよりもデータの区別が分かりやすくなっていそうな気がします。次元削減によりどうしても情報量は落ちてしまうので、3次元での可視化も上手く活用していけると良いのではないでしょうか。
まとめ
Scikit-Learnを用いたPCAについて簡単に整理しました。内容も難しくないですし、参考資料や記事等も数多くあるかと思うので、詳しく知りたい場合は丁寧に書いてあるものをきっちり読むのが良いかと思います。より発展的な手法についても今後扱っていくつもりなので、まずは第一歩としてのPCAでした。
その他
次元削減手法として、PCAと並んで頻繁に紹介されるt-SNEの解説を書いたのでこちらもよければどうぞ。
t-SNEはPCAとは違って非線型変換であり、考え方も全く異なるので、手法を知る上で参考になるかと思います。

参考文献
- 平井有三、「はじめてのパターン認識」、2012、森北出版、 https://www.morikita.co.jp/books/book/2235
- sklearn.decomposition.PCAのドキュメント
- https://www.quora.com/Is-standardization-and-normalization-the-same-in-PCA-When-should-or-should-not-we-normalize-data-in-PCA
- https://scikit-learn.org/stable/auto_examples/datasets/plot_iris_dataset.html#sphx-glr-auto-examples-datasets-plot-iris-dataset-py
- https://archive.ics.uci.edu/ml/datasets/wine+quality
- https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html